Assignment 12:

Body Fat Percentage

by

Jenny Johnson

Why would this activity appeal to students?

Popular health books often suggest that people can assess their health status by determining their percentage of body fat. Since the actual process to determine one’s body fat percentage is a complicated, expensive procedure requiring sophisticated tools, it is not practical for everyone to calculate it. The exploration of this data set with Excel will allow students to use easy, practical body measurements to make predictions about actual body fat percentage.

I found a data set at http://lib.stat.cmu.edu/datasets/bodyfat that lists the body fat percentage of 252 men based on an underwater weighing and also includes the circumference measurements for various body parts of those same 252 men. There are a total of 15 variables included in the data set which include age, weight, height, neck circumference, chest circumference, abdomen circumference and hip circumference. I then entered the data from the internet into a spreadsheet on Excel. Data for seven of the subjects is shown below.

How could we analyze the data in Excel?

We can make scatterplots in Excel with any of the variables listed in the dataset as the explanatory variable and the body fat percentage as the response variable. Since there is data for so many subjects, it is easiest to construct this scatterplot with technology. The scatterplot with wrist circumference as the explanatory variable and body fat percentage as the response variable is shown below.

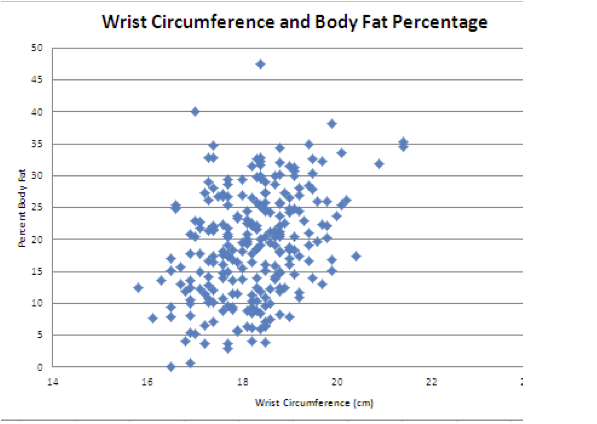
We can examine the strength of the association between the two variables by finding the line of best fit and the correlation coefficient.

Thus, Excel calculates the line of best fit and the correlation coefficient, r = .346575.

What accurately would the thigh circumference predict the body fat percentage?

First we construct a scatterplot with thigh circumference as the explanatory variable and body fat percentage as the response variable.

Now let us construct a line of best fit on Excel and calculate the correlation coefficient.

The correlation coefficient r is .559608. Thus, the thigh circumference is a better predictor of body fat percentage than wrist circumference.

What does the correlation coefficient mean in these explorations?

In generic terms, a correlation coefficient measures the strength of the linear relationship between two variables. In this situation, the correlation coefficient measures how well the circumference measurement linearly predicts a person’s body fat percentage. Since an r of 1 means the two variables have complete linear dependence and 0 means the two variables have no correlation, then a number closer to 1 indicates a stronger association. Thus, thigh circumference was a better predictor of body fat percentage than wrist circumference because .559608 is closer to 1 than .346575.

Which variable would be the best predictor of body fat percentage?

The table gives us the following possible predictors: age, weight, height, neck circumference, chest circumference, abdomen circumference, hip circumference, thigh circumference, knee circumference, ankle circumference, bicep circumference, forearm circumference, and wrist circumference. At first glance, we could eliminate age and height since one’s body fat percentage would not depend on either. We could also predict that abdomen and thigh circumference might be better predictors than knee and wrist circumference.

We can calculate the correlation coefficient for all 13 of these variables to see which is the best predictor of linear dependence with body fat percentage.

The abdomen circumference has the correlation coefficient closest to 1, r = .813432285. Chest circumference with r = .70262 is also a fairly good predictor of body fat percentage.

After creating scatterplots, lines of best fit, and the correlation coefficient for each of the variables, we can discuss the following questions.

If you knew someone’s wrist circumference, would you feel comfortable predicting their body fat percentage based on the linear regression analysis we conducted?

What if you knew someone’s weight? Or height? Or neck circumference? Or chest circumference?

With which measurement would you feel most comfortable predicting someone’s body fat percentage? Why?

What is the meaning of the correlation coefficient in this analysis?

Based on these data, do you feel more comfortable predicting a man’s body fat percentage given one of his measurements or a woman’s? Why?

What else could we explore with these data?

Students could also gather data by measuring the circumference of one of their body parts listed in the chart and use the corresponding regression line to predict their own body fat percentages.

For your own explorations of the data set, click here.

Return